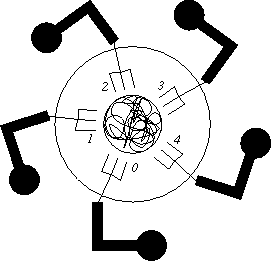
Figure 1: Deadlocked Dining Philosophers
Introduction from PhD Thesis of J.M.R Martin, University of Buckingham, UK, 1996.
Contact: Jeremy Martin
Oxford University Computing Services
13 Banbury Road
Oxford
OX2 6NN
United Kingdom
Phone: 01865 273236
Email: jeremy.martin@oucs.ox.ac.uk
Throughout our lives we take for granted the safety of complex structures that surround us. We live and work in buildings with scant regard for the lethal currents of electricity and flammable gas coarsing through their veins. We cross high bridges with little fear of them crumbling into the depths below. We are secure in the knowledge that these objects have been constructed using sound engineering principles.
Now, increasingly, we are putting our lives into the hands of complex computer programs. One could cite aircraft control systems, railway signalling systems, and medical databases as examples. But whereas the disciplines of electrical and mechanical engineering have long been well understood, software engineering is in its infancy. Unlike other fields, there is no generally accepted certification of competence for its practitioners.
Formal scientific methods for reliable software production have been developed, but these tend to require a level of mathematical knowledge beyond that of most programmers. Engineers, in general, are usually more concerned with practical issues than with the underlying scientific theory of their particular discipline. They want to get on with the business of building powerful systems. They rely on scientists to provide them with safety rules which they can incorporate into their designs. For instance, a bridge designer needs to know certain formulae to calculate how wide to set the span of an arch - he does not need to know why the formulae work. Software engineering is in need of a battery of similar rules to provide a bridge between theory and practice.
The demand for increasing amounts of computing power makes parallel programming very appealing. However additional dangers lurk in this exciting field. In this thesis we explore ways to circumvent one particularly dramatic problem - deadlock. This is a state where none of the constituent processes of a system can agree on how to proceed, so nothing ever happens. Clearly we would desire that any sensible system we construct could never arrive at such a state, but what can we do to ensure that this is indeed the case?
We might think to use a computer to check every possible state of the system. But, given that the number of states of a parallel system usually grows exponentially with the number of processes, we would most likely find the task too great. Perhaps we would conduct experimental tests to try to induce deadlock. This approach would reveal any obvious problems, but there might be deadlocks that require many years of running time to appear which we would never detect. We could attempt to construct a mathematical proof of deadlock-freedom, but we would soon discover that, even for small programs, this is often extremely difficult and time-consuming. The problem with all these approaches is that the deadlock issue has been left to the end of the software development process, when it is really too late. Design rules are needed, which may be applied a priori: rules which guarantee deadlock-freedom, are not too restrictive, and are easy to follow.
Early work in concurrency was framed in the context of multitasking operating systems. The idea was to share an expensive collection of hardware resources between a number of user processes. The classic illustration of the risk of deadlock in this situation is the Dining Philosophers of E. W. Dijkstra (described in [Hoare 1985]).
Five philosophers sit around a table. Each has a fork to his left. An everlasting bowl of spaghetti is placed in the middle of the table. A philosopher spends most of his time thinking, but whenever he is hungry he picks up the fork to his left and plunges it into the bowl. As the spaghetti is very long and tangled he requires another fork to carry it to his mouth, so he picks up the fork to his right as well. If, on attempting to pick up either fork, he should find that it is already in use he simply waits until it becomes available again. When he has finished eating he puts down both forks and continues to think.
There is a serious flaw in this system, which is only revealed when all the philosophers become hungry at the same time. They each pick up their left-hand fork and then reach out for their right hand fork, which is not there - a clear case of deadlock as shown in Figure 1 below:

Figure 1: Deadlocked Dining Philosophers
Rules of varying complexity have been devised to tackle this problem. The simplest is to allocate to each resource a unique integer priority. Then deadlock may be avoided by ensuring that no user process ever tries to acquire a resource with higher priority than one it already holds. In the case of the Dining Philosophers we could label the forks from zero to four, clockwise around the table. Four out of the five philosophers would then have a fork of higher priority to their left than their right, and so their behaviour would conform to the rule. The fifth, however, would have fork number zero to his left and fork number four to his right, so he would break the rule. If he were to modify his behaviour to always pick up the fork to his right first, the risk of deadlock would be removed. This example illustrates the power of using design rules to prevent pathological behaviour. The theory behind this particular rule is described in Chapter 2.
As computer hardware becomes more abundant, the main issue in concurrency is no longer how to share out sparse resources between multiple tasks, but rather how best to spread a single task over multiple resources, in order to improve performance. Here a task is decomposed into processes which communicate with each other, and it is these communications which pose the threat of deadlock. Concurrent programming languages provide little safeguard against this demon. Deadlock is also a potential hazard in naturally distributed systems, such as telephone networks and control programs for complex machines. Imagine a control program for the cooling system of a nuclear reactor. The program might run smoothly for many years without problem. Unless rigorous methods had been used throughout to guarantee that the program was free from deadlock there would be no way of knowing for sure whether a particular set of conditions could one day arise that would cause it to deadlock, perhaps resulting in meltdown.
The intention of this thesis is to provide a rigorous means of engineering deadlock-free concurrent systems of arbitrary size. The approach taken is to provide a collection of design rules which may be used to guarantee freedom from deadlock. These rules are by no means complete but do offer sufficient flexibility to be applicable to a wide range of problems. A welcome bonus is that their use often leads to algorithms which are more structured and elegant than those developed by `trial and error'.
Most programmers are to some extent error-prone. With this in mind a tool has been developed to check for conformance to the design rules. It will be shown how the combined weapons of design rules and automatic verification provide a vital defence against the patient and cunning foe that is deadlock.
Chapter 1 outlines the algebraic language of CSP which is used for specifying systems of communicating processes. A summary of existing techniques for deadlock analysis using this model is provided.
Chapter 2 introduces some design rules for avoiding deadlock. These are formalised in CSP. It is shown how they may be generalised and combined to provide a coherent strategy for the design of deadlock-free systems.
Chapter 3 describes the development of a software engineering tool for deadlock analysis: Deadlock Checker. This is based on the results of the preceding chapters.
Chapter 4 comprises several interesting case studies of constructing deadlock-free concurrent systems with the occam programming language, using design rules.
We conclude with a discussion of how the design approach might be extended to a wider domain of correctness issues.
A certain amount of mathematical terminology and notation is employed, deriving from Set Theory and Logic, Partial Orders and Graph Theory. In the interests of selfcontainment, and also due to a lack of consistency in the literature, the basics of the latter two fields are summarised in appendices A and B.